Riemann geometrisi, Bernhard Riemann tarafından 19. yüzyılda geliştirilen bir matematik dalıdır. Bu dal, eğri uzaylarda geometriyi incelemekle ilgilenir. Eğri uzaylar, düzlem gibi düz olmayan manifoldlardır. Örneğin, bir kürenin yüzeyi bir eğri uzaydır.
Riemann geometrisi, genel görelilik teorisinin temelini oluşturur. Genel görelilik teorisi, Albert Einstein tarafından geliştirilen bir kütleçekim teorisidir. Bu teoriye göre, kütleçekim, uzay zamanın eğriliği olarak yorumlanır. Riemann geometrisi, bu eğriliği matematiksel olarak tanımlamak ve incelemek için kullanılır.
Riemann Geometrisinin Temel Kavramları
- Manifold: Bir manifold, her noktasının bir komşuluk sistemine sahip olduğu ve bu komşuluk sistemlerinin birbiriyle uyumlu olduğu bir topolojik uzaydır. Düzlem ve küre gibi manifoldların örnekleri vardır.
- Metrik: Bir metrik, bir manifold üzerinde iki nokta arasındaki mesafeyi ölçen bir fonksiyondur. Örneğin, düzlemdeki Öklid metrik, iki nokta arasındaki mesafeyi düz çizgi uzaklığı olarak tanımlayan bir metriktir.
- Geodezik: Bir geodezik, bir manifold üzerinde iki noktayı birleştiren en kısa yoldur. Örneğin, düzlemdeki düz çizgiler geodeziklerdir.
- Riemann eğriliği: Riemann eğriliği, bir manifoldun eğriliğini ölçen bir tensördür. Riemann eğriliği, bir manifoldun geodeziklerinin ne kadar büküldüğünü gösterir.
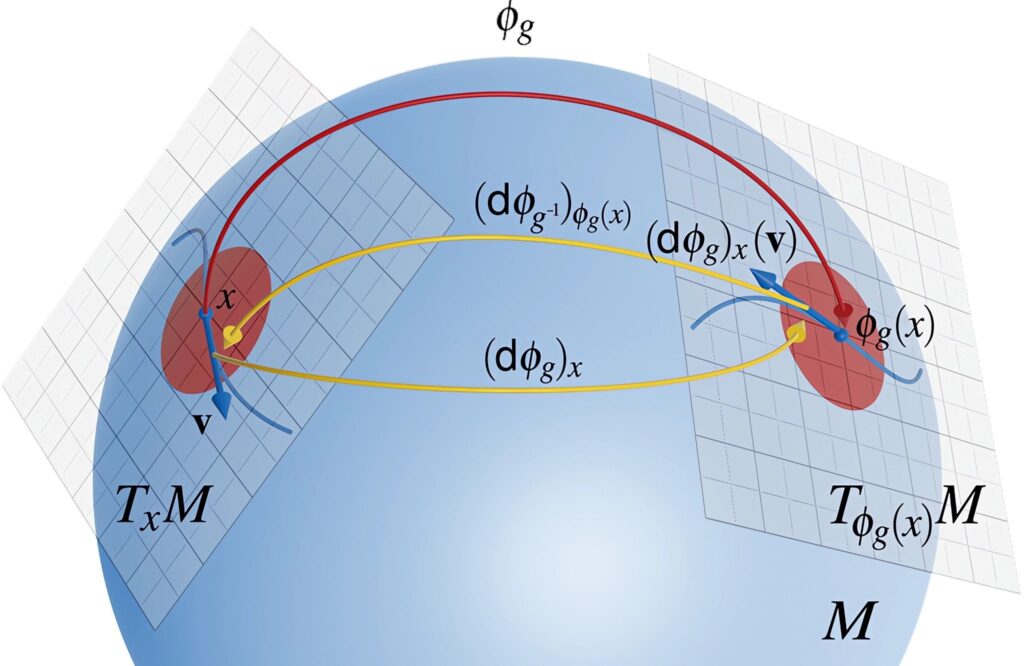
Riemann Geometrisinin Uygulamaları
- Genel görelilik teorisi: Bu teoriye göre, kütleçekim, uzay zamanın eğriliği olarak yorumlanır. Bu eğriliği matematiksel olarak tanımlamak ve incelemek için kullanılır.
- Diferansiyel geometri: Diferansiyel geometri, manifoldların geometrik özelliklerini incelemekle ilgilenir.
- Akışkanlar mekaniği: Akışkanlar mekaniği, akışkanların hareketini inceleyen bir fizik dalıdır. Akışkanların hareketini tanımlamak için kullanılan denklemleri çözmek için kullanılabilir.
- Bilgisayar grafikleri: Bilgisayar grafikleri, görüntülerin ve videoların bilgisayar tarafından oluşturulmasını inceleyen bir bilgisayar bilimi dalıdır. Üç boyutlu nesneleri ve ortamları gerçekçi bir şekilde modellemek için kullanılabilir.
Daha Fazla Bilgi Edinmek için:
- Ders Kitapları:
- “Riemannian Geometry” by Jeffreys, Barton, & Marsden
- “An Introduction to Riemannian Geometry” by Cheeger & Eisenhart
- “Riemannian Geometry and General Relativity” by Carroll
- Makaleler:
- “A Gentle Introduction to Riemannian Geometry” by Michael Spivak
- “Riemannian Geometry: A Beginner’s Guide” by Peter Petersen
- “What is Riemannian Geometry?” by Steven Wolfram